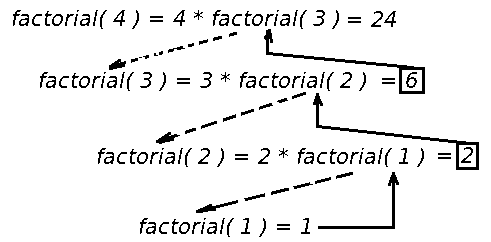
Figura 1: Representación gráfica del proceso recursivo del cálculo factorial para n = 4
Existen dos tipos de algoritmos: los iterativos (básicamente, utilizan bucles para resolver los problemas), y recursivos (se llaman a sí mismos para resolver problemas).
En cuanto a funcionalidad, los algoritmos más básicos son los de búsqueda y ordenación. En este documento se describirán dos algoritmos de este tipo, el de búsqueda binaria y el de ordenación por inserción (y el de búsqueda lineal, casi no tenido en cuenta por simple). Posteriormente, se aplicarán como ejemplo para introducir los algoritmos de tipo recursivo.
La búsqueda lineal consiste en, dado un vector o matriz, recorrerlo desde el principio hasta el final, de elelemento en elemento. Supóngase un vector que almacena cadenas: la búsqueda lineal consistirá en revisar todos los elementos hasta encontrar el que se busca. Entonces, se devuelve su posición, o -1 en caso de no ser encontrado.
ALGORITMO BúsquedaLineal
CONSTANTES
MaxElementos : ENTERO = 100
TIPOS
Vector = vector[MaxElementos] de ENTERO
FUNCION busquedaLineal(E v: Vector, numBuscado, numElem: ENTERO) : ENTERO
VARIABLES
i: ENTERO
INICIO
i ← 0
MIENTRAS v[ i ] <> numBuscado
Y i < numElem
i ← i + 1
FIN_MIENTRAS
SI i >= numElem
i ← -1
FIN_SI
RETORNAR i
FIN_FUNCION
VARIABLES
v: Vector
num: ENTERO
pos: ENTERO
INICIO
{ Preparar el vector }
DESDE i ← 0 HASTA MaxElementos - 1
v[ i ] ← i * 2
FIN_DESDE
{ Buscar }
LEER( num );
pos = busquedaLineal( v, num, MaxElementos );
{ Informar }
SI pos > -1
ESCRIBIR( “Encontrado en “, pos )
SINO ESCRIBIR( “No encontrado” )
FIN_ALGORITMO
El funcionamiento del algoritmo es obvio: primero se le da al vector de enteros valores iniciales, y después se le pide un número al usuario. Si la búsqueda lineal devuelve -1, entonces es que no se encontró; en otro caso, se devuelve la posición en la que se encontró.
El único problema que tiene este algoritmo es que depende directamente de la longitud del vector. En este caso, sea como sea la máquina donde se ejecute, su velocidad de ejecución dependerá de MaxElementos.
A continuación, se incluye la implementación en jC de este algoritmo.
* @brief Demuestra el uso de la busqueda lineal
* @author jbgarcia@uvigo.es
*/
import std.io;
import std.util;
import std.string;
int busquedaLineal(int[] v, int numBuscado)
{
int i = 0;
for(; i < size( v ); ++i) {
if ( v[ i ] == numBuscado ) {
break;
}
}
if ( i >= size( v ) ) {
i = -1;
}
return i;
}
int main()
{
int i;
int num;
int pos;
final int MaxElementos = 100;
int[] v = new int[MaxElementos];
// Prepara el vector
for(i = 0; i < MaxElementos; ++i) {
v[ i ] = i * 2;
}
// Pide el número a buscar
num = strToInt( readln( "Introduzca un número a buscar: " ) );
pos = busquedaLineal( v, num );
// Informa
if ( pos > -1 ) {
print( "\nEncontrado en: " );
println( pos );
} else {
println( "\nNo encontrado." );
}
return 0;
}
La búsqueda binaria consiste en, dado un vector, comprobar la mitad del vector, con lo que, según el elemento a buscar, estará en una de las mitades. Este proceso se repite con la mitad donde esté el elemento, comprobando si el medio es el elemento buscado, y así sucesivamente hasta encontrarlo (de estar). Ésto implica una limitación básica para que este algoritmo pueda funcionar: el vector tiene que haberse ordenado previamente, sus elementos deben estar ordenados para poder elegir la mitad correcta en la que buscar a continuación. Como el algoritmo anterior, devuelve la posición o -1 en caso contrario.
ALGORITMO BúsquedaBinaria
CONSTANTES
MaxElementos : ENTERO = 100
TIPOS
Vector = vector[MaxElementos] de ENTERO
FUNCION busquedaBinaria(E v: Vector, numBuscado, numElem: ENTERO) : ENTERO
VARIABLES
alto: ENTERO
bajo: ENTERO
medio: ENTERO
INICIO
alto = numElem;
bajo = 0;
medio = bajo + ( ( alto – bajo ) / 2 )
MIENTRAS v[ medio ] <> numBuscado
Y medio > bajo
SI numBuscado > v[ medio ]
bajo = medio
SINO
alto = medio
FIN_SI
medio = bajo + ( ( alto – bajo ) / 2 )
FIN_MIENTRAS
SI v[ medio ] != numBuscado
medio ← -1
FIN_SI
RETORNAR medio;
FIN_FUNCION
VARIABLES
v: Vector
num: ENTERO
pos: ENTERO
INICIO
{ Preparar el vector }
DESDE i ← 0 HASTA MaxElementos - 1
v[ i ] ← i * 2
FIN_DESDE
{ Buscar }
LEER( num );
pos = busquedaBinaria( v, num, MaxElementos );
{ Informar}
SI pos > -1
ESCRIBIR( “Encontrado en “, pos )
SINO ESCRIBIR( “No encontrado” )
FIN_ALGORITMO
El funcionamiento del algoritmo es obvio: primero se le da al vector de enteros valores iniciales, y después se le pide un número al usuario. Si la búsqueda binaria devuelve -1, entonces es que no se encontró; en otro caso, se devuelve la posición en la que se encontró.
A continuación, se incluye la implementación en C++ estructurado de este algoritmo.
/**
* @name Busqueda Binaria
* @author jbgarcia@uvigo.es
*/
import std.io;
import std.util;
import std.string;
final int MaxElementos = 100;
int busquedaBinaria(int[] v, int numBuscado, int numElem)
{
int alto = numElem;
int bajo = 0;
int medio = bajo + ( ( alto - bajo ) / 2 );
int toret = -1;
while( v[ medio ] != numBuscado
&& medio > bajo )
{
if ( numBuscado > v[ medio ] ) {
bajo = medio;
} else {
alto = medio;
}
medio = bajo + ( ( alto - bajo ) / 2 );
}
if ( v[ medio ] == numBuscado) {
toret = medio;
}
return toret;
}
int main()
{
int i;
int num;
int pos;
int[] v = new int[MaxElementos];
// Preparar el vector
for(i = 0; i < MaxElementos; ++i) {
v[ i ] = i * 2;
}
// Pedir el num y buscar
print( "Nums. entre 0 y " );
println( ( MaxElementos -1 ) * 2 );
num = strToInt( readln( "Introduzca un num. a buscar: " ) );
pos = busquedaBinaria( v, num, MaxElementos );
// Informar
if ( pos > -1 ) {
print( "\nEncontrado en " );
println( pos );
} else {
println( "\nNo encontrado.\n" );
}
return ExitSuccess;
}
El rendimiento mejora ampliamente al del algoritmo anterior. Ahora, el tiempo de ejecución sólo depende del número de veces que el número total de elementos del vector pueda dividirse entre 2, es decir log2 MaxElementos. El único problema que presenta es que es necesario tener el vector ordenado previamente.
La ordenación por inserción precisa del doble de memoria de la que el vector ocupa. En un segundo vector, en principio vacío (aunque del mismo tamaño máximo que el primero), se van introduciendo los elementos del primero, secuencialmente, pero insertándolos de manera ordenada. Al final del recorrido del vector original, todos los elementos estarán ordenados en el segundo vector.
ALGORITMO OrdenaciónPorInserción
CONSTANTES
MaxElementos : ENTERO = 100
TIPOS
Vector = vector[MaxElementos] de ENTERO
PROCEDIMIENTO ordenaInsercion(E/S v: Vector, E numElem: ENTERO)
VARIABLES
i: ENTERO
j: ENTERO
k: ENTERO
v2: Vector
numOcupados: ENTERO
INICIO
numOcupados ← 0
{ Preparar el vector }
DESDE i ← 0 HASTA MaxElementos - 1
v2[ i ] ← v[ i ]
FIN_DESDE
{ Insertar ordenadamente }
DESDE i ← 0 HASTA numElem – 1
{ buscar la pos }
j ← 0
MIENTRAS j < numOcupados
Y v[ i ] > v2[ j ]
j ← j + 1
FIN_MIENTRAS
{ desplazar el vector }
DESDE k ← numOcupados HASTA j
v[ k + 1 ] = v[ k ];
FIN_DESDE
{ insertar ordenado en vector }
numOcupados ← numOcupados + 1
v[ j ] = v2[ i ];
FIN_DESDE
FIN_FUNCION
VARIABLES
v: Vector
num: ENTERO
pos: ENTERO
i: ENTERO
INICIO
{ Preparar el vector }
DESDE i ← 0 HASTA MaxElementos
SI ( ( i mod 2 ) == 0 )
v[ i ] ← i / 2;
SINO v[ i ] ← i * 2
FIN_DESDE
{ Ordenar }
LEER( num );
ordenaInsercion( v, MaxElementos );
{ Informar }
DESDE i ← 0 HASTA MaxElementos
ESCRIBIR( v[ i ] )
FIN_DESDE
FIN_ALGORITMO
El funcionamiento del algoritmo es obvio: primero se le da al vector de enteros valores iniciales desordenados, y entonces el vector se ordena, mostrándole el resultado al usuario.
A continuación, se incluye la implementación en jC de este algoritmo.
/**
* @name Orderna insertando
* @author jbgarcia@uvigo.es
*/
import std.io;
import std.util;
import std.string;
void ordenaInsercion(int[] v)
{
int posVorg;
int posDesp;
int posOrd;
int numOcupados = 0;
int numElem = size( v );
int[] v2 = new int[numElem];
// Preparar el vector auxiliar
for(posVorg = 0; posVorg < numElem; ++posVorg) {
v2[ posVorg ] = v[ posVorg ];
}
// Insertar ordenadamente
for(posVorg = 0; posVorg < numElem; ++posVorg) {
// buscar la pos
posOrd = 0;
while ( posOrd < numOcupados
&& v2[ posVorg ] > v[ posOrd ] )
{
++posOrd;
}
// desplazar el vector
for(posDesp = numOcupados; posDesp > posOrd; --posDesp) {
v[ posDesp + 1 ] = v[ posDesp ];
}
// insertar ordenado en vector
++numOcupados;
v[ posOrd ] = v2[ posVorg ];
}
return;
}
int main()
{
int i;
int num;
int pos;
final int MaxElementos = 100;
int[] v = new int[MaxElementos];
// Preparar el vector
for(i = 0; i < MaxElementos; ++i) {
if ( ( i % 2 ) == 0 ) {
v[ i ] = 120 + ( i / 2 );
} else {
v[ i ] = 120 + ( i * 2 );
}
}
// Pedir el num y buscar
ordenaInsercion( v );
// Informar
for(i = 0; i < MaxElementos; ++i) {
print( v[ i ] );
print( ' ' );
}
println();
return 0;
}
La velocidad de ejecución mejora ampliamente la alternativa más simple, que es el algoritmo de la burbuja (no explicado en este documento). Es necesario tener en cuenta, sin embargo, que este algoritmo es una variación del original: se utiliza un vector de destino, en un principio vacío, para evitar en lo posible que la eficiencia dependa del cuadrado de MaxElementos.
La velocidad de ejecución del algoritmo de ordenación por la burbuja depende de MaxElementos2, mientras que en este caso suele comportarse, en media, mucho mejor que el de la burbuja, si bien, en el peor de los casos (curiosamente, que el vector ya esté ordenado, pero a la inversa), es cierto que tambíen depende de MaxElementos2.
Los algoritmos recursivos se denominan de esta forma debido a que se llaman a sí mismos para completar una ejecución. Hacer esto sin control de ningún tipo supondría un error de ejecución, ya que el programa se quedaría eternamente llamando a la misma función. Por eso, en un algoritmo recursivo es necesario prestar atención a dos casos:
El caso base, el que termina la recursión.
El caso repetitivo, el que realiza la recursión.
Un ejemplo típico es el cálculo del factorial de un número. El factorial de un número n, factorial( n ), puede entenderse como n * factorial( n – 1 ), siempre y cuando se tenga en cuenta que factorial( 1 ) es 1, es decir, no provoca ninguna llamada recursiva. Este último caso es el caso base. El primero, n ← n * factorial( n – 1 ), es el caso repetitivo.
El algoritmo recursivo de cálculo del factorial sería, por tanto:
FUNCION factorial(E n: ENTERO) : ENTERO
INICIO
SI ( n == 1 )
factorial ← 1
SINO
factorial ← n * factorial( n – 1 )
FIN_SI
FIN_FUNCION
Esta misma función, en jC sería:
int factorial(int n)
{
int toret = 1;
if ( n > 1 ) {
toret = n * factorial( n - 1 );
}
return toret;
}
La sucesión de llamadas si se lanzase la ejecución con n = 4, sería la siguiente:
1: factorial( 4 )
2: factorial( 3 )
3: factorial( 2 )
4: factorial( 1 )
Se detendría en factorial( 1 ) porque esta llamada no provoca ninguna llamada recursiva, sino que ya es el caso base: devuelve 1. Es ahora cuando se produce el primer retorno.
La cuarta llamada devuelve 1, por lo que la tercera llamada factorial( 2 ), puede ya continuar su ejecución, sólo tiene que sustituir la expresión en la que estaba suspendida: n * factorial( n -1). n es 2, y la llamada recursiva acaba de devolver 1, por lo que la llamada tercera devuelve el resultado de multiplicar 2 * 1, a la segunda llamada, factorial( 3 ).
Esta llamada se había quedado suspendida mientras se calculaba factorial( 2 ), en la ya conocida expresión n * factorial( n -1), puesto que n es 3. La expresión, por tanto, queda finalmente como 3 * 2, que es lo que la segunda llamada devuelve a la primera, la que inició el proceso, que se había quedado suspendida en el mismo punto que las otras.
Para esta primera llamada n es 4, y factorial( 3 ) acaba de devolver 6, por lo que la expresión n * factorial( n -1), quedaría como 4 * 6, que es el resultado que finalmente devolvería la primera llamada, la que inicio la ejecución.

Figura 1: Representación
gráfica del proceso recursivo del cálculo factorial
para n = 4
Un ejercicio similar al anterior sería el de la suma. Supóngase que no existe el operador '*', y por lo tanto la multiplicación se debe programar. La versión iterativa de este ejercicio sería:
FUNCION multiplicacion(E a, b: ENTERO) : ENTERO
i: ENTERO
resultado: ENTERO
INICIO
resultado ← 0
DESDE i ← 0 HASTA b - 1
resultado ← resultado + a
FIN_DESDE
suma ← resultado
FIN_FUNCION
Pero esta función podría transformarse en recursiva, si se tiene en cuenta que la multiplicacion( a, b ) puede entenderse recursivamente como 0 cuando b == 0 y como a + multiplicacion( a, b – 1 ) en el resto de casos.
FUNCION multiplicacion(E a, b: ENTERO) : ENTERO
INICIO
SI b = 0
multiplicacion ← 0
SINO
multiplicacion ← a + multiplicacion( a, b – 1 )
FIN_SI
FIN_FUNCION
Así, la multiplicación de tres por cuatro supondría las siguientes llamadas recursivas (los valores entre corchetes son las operaciones que se realizan una vez llegados hasta la base de la recursión):
multiplicacion( 3, 4 ) = 3 + multiplicacion( 3, 3 ) [=3 + 6]
multiplicacion( 3, 3 ) = 3 + multiplicacion( 3, 2 ) [= 3 + 6]
multiplicacion( 3, 2 ) = 3 + multiplicacion( 3, 1 ) [= 3 + 3]
multiplicacion( 3, 1 ) = 3 + multiplicacion( 3, 0 ) [= 3 + 0]
multiplicacion( 3, 0 ) [= 0]
La programación del algoritmo en jC es prácticamente directa:
int multiplicacion(int a, int b)
{
int toret = 0;
if ( b > 0 ) {
toret = a + multiplicacion( a, b – 1 );
}
return toret;
}
La búsqueda binaria es, por su propia naturaleza, recursiva: se busca el elemento en una mitad, después en otra, dentro de la misma, hasta que finalmente se encuentra (o no). La transformación de este algoritmo en recursivo depende por tanto de las variables alto y bajo, que por tanto deben pasar a formar parte de los parámetros de la función.
FUNCION busquedaBinaria(E v: Vector, numBuscado, bajo, alto: ENTERO) : ENTERO
VARIABLES
medio: ENTERO
INICIO
medio = bajo + ( ( alto – bajo ) / 2 )
SI v[ medio ] <> numBuscado
SI medio == bajo
medio ← -1
SINO
SI numBuscado > v[ medio ]
bajo = medio
SINO
alto = medio
FIN_SI
medio = busquedaBinaria( v, numBuscado, bajo, alto );
FIN_SI
FIN_SI
busquedaBinaria ← medio
FIN_FUNCION
El modo de trabajo de esta función recursiva es el mismo que el de la versión iterativa, con la diferencia de que cada llamada se encarga de sólo una mitad del vector donde buscar, y en caso de no encontrar el elemento buscado, realiza una llamada recursiva hacia otra de las mitades. El proceso, para un vector de cuatro posiciones, en el que se busca el 10, sería el siguiente:
|
5 |
10 |
15 |
20 |
busquedaBinaria( v, 10, 0, 4 ) [=1]
busquedaBinaria( v, 10, 0, 2 ) [= 1]
En cursiva se marcan los valores que se retornan después del retorno del caso base. ¿Qué sucedería si el elemento a buscar fuese el 11?
busquedaBinaria( v, 10, 0, 4 ) [=-1]
busquedaBinaria( v, 10, 0, 2 ) [=-1]
busquedaBinaria( v, 10, 0, 1 ) [ =-1]
Nótese que al ser división entera (puesto que los miembros de la expresión son enteros), el resultado de dividir 1 / 2 es 0.
A continuación, se incluye el código fuente en jC:
/**
* @name BusquedaBinariaRecursiva
* @author jbgarcia@uvigo.es
*/
import std.io;
import std.util;
import std.string;
int busquedaBinaria(int[] v, int numBuscado, int bajo, int alto)
{
int medio = bajo + ( ( alto - bajo ) / 2 );
if ( v[ medio ] != numBuscado ) {
if ( medio == bajo ) {
medio = -1;
} else {
if ( numBuscado > v[ medio ] ) {
bajo = medio;
} else {
alto = medio;
}
medio = busquedaBinaria( v, numBuscado, bajo, alto );
}
}
return medio;
}
int main()
{
final int MaxElementos = 100;
int i;
int num;
int pos;
int[] v = new int[MaxElementos];
// Preparar el vector
for(i = 0; i < MaxElementos; ++i) {
v[ i ] = i * 2;
}
// Pedir el num y buscar
num = strToInt( readln( "Introduzca un número a buscar: " ) );
pos = busquedaBinaria( v, num, 0, MaxElementos );
// Informar
if ( pos > -1 ) {
print( "\nEncontrado en: " );
println( pos );
} else {
println( "\nNo encontrado.\n" );
}
return 0;
}
En este tema se han visto algoritmos básicos de búsqueda y ordenación, a la vez que se ha introducido la recursividad. Tal y como se ha visto, el resultado es el mismo en ambos casos, sea el algoritmo recursivo o iterativo, y su eficiencia teórica no cambia.
Un factor que sí se debe tener en cuenta es que el algoritmo recursivo supone realizar llamadas a funciones en lugar de iteraciones de bucles, y en general lo primero es bastante más complejo, y consume más recursos (como memoria en la pila de llamadas) que lo segundo.
Siendo así, es posible plantearse siquiera la necesidad de utilizar algoritmos recursivos. Las ventajas de estos algoritmos no radican en su eficiencia, sino en la superior abstracción que se obtiene con ellos (es decir, el diseño de ciertos algoritmos complejos se hace más sencillo).
Supóngase el siguiente ejemplo: una calculadora debe evaluar expresiones como (6+(5*4)) / 2, de manera que siempre haya una pareja de paréntesis antes de cada subexpresión, y no se incluyan espacios. Por supuesto este problema se puede resolver de manera iterativa, pero de manera recursiva la solución es mucho más simple, como se puede ver a continuación:
ALGORITMO Calculadora
FUNCION calcular(E operando1: ENTERO, operador: CARACTER, operando2: ENTERO) : ENTERO
VARIABLES
resultado: ENTERO
INICIO
{ Prec. Operador = '*' O '/', O '+' O '-' }
CASO DE operador
'*': resultado ← operando1 * operando2
'/': resultado ← operando1 / operando2
'+': resultado ← operando1 + operando2
'-': resultado ← operando1 – operando2
FIN_CASO
calcular ← resultado
FIN_FUNCION
FUNCION evaluar(E expresion: Cadena, E/S pos: ENTERO) : ENTERO
VARIABLES
operando1: ENTERO
operando2: ENTERO
operador: CARACTER
INICIO
{ tomar primer operando }
SI expresion[ pos ] = '('
pos ← pos + 1
operando1 = evaluar( expresion, pos )
pos ← pos + 1
SINO
operando1 = convertirCadenaNumero( expresion, pos )
FIN_SI
{ tomar operador }
operador = expresion[ pos ]
pos ← pos + 1
{ tomar segundo operando }
SI expresion[ pos ] = '('
pos ← pos + 1
operando2 = evaluar( expresion, pos )
pos ← pos + 1
SINO
operando2 = convertirCadenaNumero( expresion, pos )
FIN_SI
evalua ← calcular( operando1, operador, operando2 )
FIN_FUNCION
FUNCION convertirCadenaNumero( E entrada : CADENA, E/S pos:ENTERO)
VARIABLES
aux: CADENA
INICIO
MIENTRAS entrada[ pos ] >= '0'
Y entrada[ pos ] <= '9'
Y pos < longitud( cadena )
aux ← aux + entrada[ pos ]
pos ← pos + 1
FIN_MIENTRAS
convertirCadenaNumero ← convertirANumero( aux ) { atoi( aux ) en C++ }
FIN_FUNCION
FUNCION evaluarExpresion(E entrada: CADENA) : ENTERO
VARIABLES
pos: ENTERO
INICIO
pos ← 0
evaluarExpresion ← evaluar( entrada, pos )
FIN_FUNCION
VARIABLES
entrada: CADENA
INICIO
LEER( entrada );
ESCRIBIR( resultado, evaluarExpresion( entrada ) )
FIN_ALGORITMO
La función convertirANumero() se ha marcado en negrita porque depende del lenguaje de programación utilizando. En C++, esta función sería exactamamente atoi(), (convierte una cadena con un número en su interior a ese número). Las llamadas recursivas que se producirían para una la expresión matemática anterior, serían las indicadas en la figura 2.
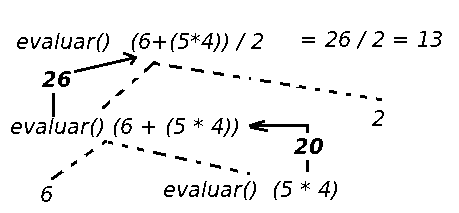
Figura 2: Esquema de ejecución de la calculadora:
evaluar( 5 * 4) es la base de la recusión en este ejemplo.
Crea una función recursiva que permita elevar un número entero cualquiera a otro.
Crea una pequeña aplicación estadística que permita introducir datos de temperaturas en un determinado período, y los presente ordenados.