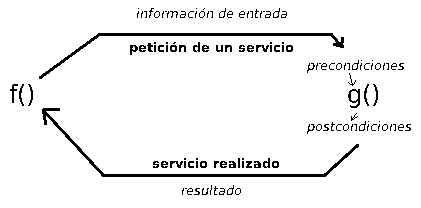
Figura 1: Esquema básico de funcionamiento: f llama a g, por lo que g realiza un servicio para f.
Las ideas del Diseño o programación por Contrato, tienen sus raíces en los métodos formales para la construcción de software, pero mantienen una visión más pragmática. Requieren muy poco esfuerzo extra pero generan software mucho más confiable. La idea fue introducida en una fecha tan temprana como 1992 por Bertrand Meyer, y su lenguaje de programación Eiffel.
La programación por contrato puede ser imaginada como la aplicación a la construcción de software de los contratos que rigen los asuntos de las personas. Cuando dos personas establecen un contrato se desprenden de éste, las obligaciones y beneficios de cada una.
Si ahora trasladamos estos conceptos al diseño del software, lo que se busca obtener es que este tipo de contratos en software especifican, en forma no ambigua, las relaciones entre las rutinas y los llamadores de las mismas. Así, un sistema sería como un conjunto de elementos de software interrelacionados, donde cada uno de los elementos tiene un objetivo con vistas a satisfacer las necesidades de los otros. Dichos objetivos son los contratos. Los contratos deben cumplir, por lo menos, con dos propiedades: ser explícitos y formar parte del elemento de software en sí mismo.
El Diseño por Contrato da una visión de la construcción de sistemas como un conjunto de elementos de software cooperando entre sí. Los elementos juegan en determinados momentos alguno de los dos roles principales proveedores o clientes. La cooperación establece claramente obligaciones y beneficios, siendo la especificación de estas obligaciones y beneficios los contratos. Un contrato entre dos partes protege a ambas. Por un lado protege al cliente por especificar cuanto debe ser hecho y por el otro al proveedor por especificar el mínimo servicio aceptable.
Los contratos de software se especifican mediante la utilización de expresiones lógicas denominadas aserciones. En el Diseño por Contratos se utilizan dos tipos de aserciones:
• Precondiciones
• Poscondiciones
Se denominan aserciones porque son condiciones que deben cumplirse. Su incumplimiento invalida totalmente el software, hace que éste deje de trabajar, pues el incumplimiento de un contrato, como se vé en la figura 1, indica que existe un error en el programa.

Figura 1: Esquema básico de funcionamiento: f
llama a g, por lo que g realiza un servicio para f.
{ P } A { Q }
representa lo que se llama fórmula de corrección. La semántica de dicha fórmula es la siguiente: cualquier ejecución de A que comience en un estado en el cual se cumple P dará como resultado un estado en el cual se cumple Q. Por ejemplo
{ Prec.: longitud( str1 ) > 4 }
subcadena( str1, 0, 4, str2 );
{ Postc.: longitud( str2 ) == 4 }
En este ejemplo, se parte de un estado en el que la cadena str1 debe tener más de cuatro caracteres, puesto que se van a extraer para guardarlos en la cadena str2. La precondición (P, como se la mencionaba antes), precisamente, trata de asegurar que ese estado sea exactamente el estado de partida, comprobando si la cadena tiene al menos cuatro caracteres. Entonces se ejecuta la tarea, (extraer una subcadena de otra), y la postcondición (Q, tal y como se mencionaba antes) trata de verificar que el trabajo se ha cumplido correctamente (si se han extraído cuatro caracteres de str1, debería haber cuatro caracteres en str2).
Por supuesto, este ejemplo es trivial. Ningún programador haría precondiciones y postcondiciones para una tarea tan sencilla como ésta (aunque la precondición nunca estaría de más).
Para obtener los beneficios de este tipo de diseño, se pueden recordar una serie de pasos a seguir:
Separar consultas de comandos. Este principio también fue inicialmente explicado detalladamente en Meyer. La idea es que las rutinas de una clase deben ser (en lo posible) o comandos o consultas pero no ambas cosas. Las consultas devuelven un valor (ej. funciones) y los comandos pueden cambiar el estado interno del objeto.
Separar consultas básicas de consultas derivadas. La intención es conseguir un conjunto de especificación formado por consultas que denominamos básicas, de tal forma que el resto de las consultas puedan derivarse de las básicas.
Para cada consulta derivada escribir una poscondición especificando su resultado en términos de una o más consultas básicas. Esto permite conocer el valor de las consultas derivadas conociendo el valor de las consultas básicas. Idealmente, sólo el conjunto minimal de especificación tiene la obligación de ser exportado públicamente.
Para cada comando escribir una precondición que especifique el valor de cada consulta básica. Dado que el resultado de todas las consultas puede visualizarse a través de las consultas básicas, con este principio se garantiza el total conocimiento de los efectos visibles de cada comando.
Para toda consulta o comando decidir una precondición adecuada. Este principio se auto explica ya que permite definir claramente el contrato de cada rutina.
En el siguiente ejemplo, muy sencillo, se parte de un algoritmo en el que se leen dos númeors por teclado y se va a presentar la división de ambos números. Como es lógico, colocamos la precondición en la función dividir.
ALGORITMO división
FUNCION dividir(E dividendo, divisor: REAL): REAL
INICIO
{ Prec. divisor <> 0 }
dividir ← dividendo / divisor;
FIN_FUNCION
VARIABLES
a: REAL
b: REAL
INICIO
LEER( a )
LEER( b )
ESCRIBIR( dividir( a, b ) );
FIN_ALGORITMO
Nótese que la función dividir() podría haber sido escrito de la siguiente manera:
FUNCION dividir(E dividendo, divisor: REAL): REAL
INICIO
SI ( divisor <> 0 )
dividir ← dividendo / divisor;
SINO dividir ← 0
FIN_FUNCION
De lo que se trata es de programar defensivamente ante la aparición de un error. Aunque la programación defensiva con respecto a la aparición de errores (es decir, tener en cuenta que se pueden producir errores) es buena, no es buena idea reaccionar de esta forma, pues lo que se está haciendo en realidad es encubrir que el error ha aparecido. En un programa tan sencillo como este no habría mayores consecuencias, pero en un proyecto real este error encubierto acabaría provocando otros errores, probablemente en otros módulos de cálculo, y sería realmente difícil rastrear el error hasta el origen.
La primera regla, por tanto, a recordar, es que los errores deben detectarse en el momento más temprano que sea posible. La segunda regla es distinguir entre código de módulos, reutilizable en otras aplicaciones, y código específico para un proyecto dado (muchas veces de interfaz con el usuario), y la tercera regla distinguir entre los errores de programación en módulos, y los errores provocados por entradas del usuario.
Así, en este caso, una cierta entrada del usuario puede provocar que la aplicación aborte. Es necesario resolver esta situación, pero la función dividir() formará parte en el futuro de un módulo, por lo que la precondición está bien puesta, y no es ahí donde debemos tratar el error. La pregunta es ¿tiene sentido que a dividir() llegue un cero como parámetro?. La respuesta es no, si se hace una llamada a dividir() con un 0 para divisor, es que algo va mal y es necesario capturar ese error cuanto antes. Por tanto, la solución es:
ALGORITMO división
FUNCION dividir(E dividendo, divisor: REAL): REAL
INICIO
{ Prec. divisor <> 0 }
dividir ← dividendo / divisor;
FIN_FUNCION
VARIABLES
a: REAL
b: REAL
INICIO
LEER( a )
LEER( b )
SI b <> 0
ESCRIBIR( dividir( a, b ) );
SINO ESCRIBIR( “¡No se puede dividir por cero!” )
FIN_ALGORITMO
Las precondiciones y postcondiciones deben capturar los errores de programación, nunca tratar los errores derivados de la entrada del usuario.
Para poder implementar un ejemplo como el anterior, se utiliza una función del módulo std.util, llamada verify(), que evalúa la condición que se le pase entre paréntesis, y en caso de ser verdadera, no hace nada. En caso de evaluarse como falsa, aborta el programa indicando el mensaje que se le pasa como segundo parámetro.
A continuación, se implementará el diseño anterior en jC.
/**
@name division
@author jbgarcia@uvigo.es
*/
import std.io;
import std.util;
import std.string;
double dividir(double dividendo, double divisor)
{
verify( divisor != 0, "Imposible dividir por cero." );
return dividendo / divisor;
}
int main()
{
double a = strToDbl( readln( "Introduzca valor a dividir: " ) );
double b = strToDbl( readln( "Introduzca valor por el que dividir: " ) );
if ( b != 0 ) {
print( "\nResultado: " );
println( dividir( a, b ) );
} else {
println( "\nNo se puede dividir por cero.\n" );
}
return ExitSuccess;
}