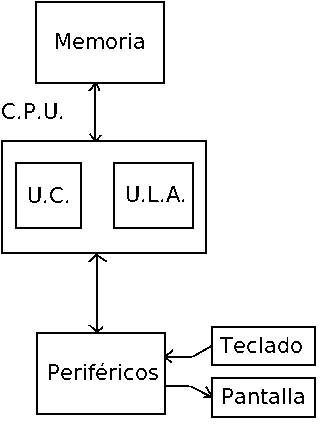
Figura 1: Esquema básico de una computadora.
Introducción a la programación
Introducción a la programación 3
2Datos, Variables y Constantes 5
2.2.2Funciones disponibles en la librería estándar 7
2.2.3Restricciones de asignación 8
2.2.4Entrada y salida de datos 8
3Paradigma de programación estructurado 10
3.3Composición de instrucciones 10
3.6Composición condicional (SI) 10
3.6.15.2.2 Composición alternativa 11
3.6.25.2.3 Composición selectiva 11
3.6.35.2.4 Equivalencias de estructuras de decisión 12
4.1Composición iterativa MIENTRAS 13
4.2Composición iterativa REPETIR 13
4.3Composición iterativa DESDE 14
4.4Equivalencia entre composiciones iterativas 14
5Otras representaciones algorítmicas 15
5.1Diagramas N-S ó Nassi Schederman 15
5.2Diagramas de flujo o flujogramas 16
6Ejemplos de algoritmos típicos 19
6.1Cálculo del máximo común divisor de un número 19
6.2Cálculo del máximo común múltiplo de un número 19
6.3Cálculo de la potencia de un número elevado a otro 19
6.4Cálculo de las areas de varias figuras 20
6.5Lectura de un número en una determinada base 21
7Traduciendo pseudocódigo a jC 22
7.1.1Comentarios, elementos básicos, y literales. 26
7.1.3Constantes y variables 27
7.1.5Descripción de las tres composiciones de programación estructurada 29
Los computadores han sido ideados para procesar información de diverso tipo de forma automatizada. La idea es que un computador similar a una máquina genérica. El programador simplemente cambia el programa o software y el computador empieza a hacer algo totalmente nuevo.

Figura 1: Esquema básico de una computadora.
Hardware: parte tangible o visible.
CPU: Central Processing Unit, o unidad central de proceso. Realiza todos los cálculos y procesos. También se la conoce como microprocesador.
Memoria: También conocida como RAM (Random Access Memory, o memoria de acceso aleatorio). En ella se guardan todos los datos.
Periféricos: controlados por la CPU, se encargan de realizar la interacción con el usuario.
Software: conjunto de programas para procesar la información (es lo que permite cambiar el proceso de datos).
Programa: conjunto de instrucciones codificadas en un lenguaje entendible para la máquina (binario).
Para realizar un programa se deben dar los siguientes pasos:
Entender el problema a resolver.
Idear un algoritmo y representarlo en notación algorítmica.
Codificar el algoritmo en un lenguaje de programación para obtener el código fuente del programa.
Mediante un proceso automático con un compilador (compiler) y un enlazador (linker) se traduce al lenguaje que entiende el computador.
Entre las definiciones de algoritmo se pueden encontrar las siguientes
Conjunto de instrucciones para realizar una tarea que se expresan en notación algorítmica.
Fórmula para resolver un problema.
Conjunto de acciones en secuencia que ejecutadas en un determinado orden resuelven un problema.
Características de los algoritmos:
Precisión: Es una secuencia de pasos que deben estar totalmente definidos.
Bien definido: Debe contemplar todos los detalles.
Tiene que ser finito (Es decir, en algún momento se termina).
Los algoritmos no se representan en lenguajes de programación, se representan con notación algorítmica. Las notaciones algorítmicas que se estudian en este curso son las siguientes:
Pseudocódigo.
Diagramas N-S o Nassi-Schederman.
Diagramas de flujo o flujogramas.
El esquema general de un algoritmo en pseudocódigo es el siguiente:
ALGORITMO <NOMBRE>
CONSTANTES
<IDENTIFICADOR C1>: <TIPO> = <VALOR C1>
.
.
<IDENTIFICADOR Cn>: <TIPO> = <VALOR Cn>
TIPOS
<IDENTIFICADOR TIPO 1>=<DEFINICIÓN TIPO 1>
.
.
<IDENTIFICADOR TIPO n>=<DEFINICIÓN TIPO n>
VARIABLES
<IDENTIFICADOR V1>: <TIPO V1>
.
.
<IDENTIFICADOR Vn>: <TIPO Vn>
INICIO
<INSTRUCCIÓN 1>
.
.
.
<INSTRUCCIÓN N>
FIN_ALGORITMO
Los ordenadores manejan la información en base a datos guardados en la memoria, que se operan en su microprocesador. Según la utilización de los datos, estos se dividen en:
Variables: datos cuyo valor varía a lo largo de la ejecución del algoritmo.
Constantes: datos cuyo valor no cambia a lo largo de la ejecución del programa.
Las variables y las constantes se definen por un identificador (un nombre que las identifica) y un tipo (descripción de los valores que mantienen).
ALGORITMO ÁreaCírculo
CONSTANTES
PI: Real = 3.1416
VARIABLES
radio: Real
resultado: Real
INICIO
LEER( radio )
resultado ← PI * radio * radio
ESCRIBIR( resultado )
FIN_ALGORITMO
Los tipos de datos más comunes se discuten a continuación:
Entero: ![]() Conjunto
de los números enteros.
Conjunto
de los números enteros.
Los límites de los números enteros que se pueden representar con este tipo de dato varían directamente según el hardware, es decir, el tamaño de palabra, del computador. En computadores de la década de los 90, con un tamaño de palabra de 16 bits, se podían representar enteros de -32,768 a 32,767, mientras que en hardware de 32 bits el rango se amplía geométricamente, abarcando desde los -2000 millones hasta los 2000 millones. El hardware de 64 bits hace que estos límites se amplíen todavía más, desde -92,233,720,368 a 92,233,720,367.
Real: ![]() Conjunto
de los números reales.
Conjunto
de los números reales.
Los números reales abarcan un gran abanico de posibilidades, estando más limitados en cuanto a precisión que en cuanto a márgenes totales.
Carácter: ‘c’ Un único carácter.
Los caracteres forman las cadenas de texto, es decir texto que está formado por secuencias de caracteres. Internamente, un carácter básico es un número que abarca desde 0 a 255.
Cadenas: “c/ Lorenzo Lamas” Secuencia de caracteres.
Las cadenas de caracteres están formadas por caracteres colocados secuencialmente en memoria, uno detrás de otro. Existen varias formas de indicar el número de caracteres almacenado: la que abanderó en su día el lenguaje de programación Pascal, con una primera posición que indicaba el tamaño de la cadena, o la más popular hoy en día, del lenguaje de programación C, que cierra la secuencia de caracteres con un carácter de valor 0 ('\0').
Lógicos: Sólo toman el valor Verdadero (true)/ Falso (false).
Los valores lógicos son retornados por expresiones booleanas, de manera que puedan concatenarse todas juntas y formar expresiones booleanas complejas. Pero también es normalmente necesario almacenar estos valores para ser empleados más tarde.
Una expresión es una combinación de constantes, variables, operadores, paréntesis y nombres de función que representan una determinada forma de operar con los datos.
La asignación es la operación por medio de la cual una variable toma el valor resultado de la evaluación de una expresión. Se representa mediante el símbolo . Ejemplo:
a 3.14;
a a + 5;
Toda la computación y los lenguajes de programación más empleados (imperativos) giran en torno a esta operación.
Los operadores permiten combinar los datos para realizar los cálculos necesarios para llevar a cabo la acción que se desea. Los operadores pueden ser de dos tipos:
Unarios: se aplican sólo sobre un dato, por ejemplo: negación lógica: ¬a
Binarios: se aplican sobre dos datos, por ejemplo: suma 5 + a siendo a Entero o Real.
A continuación se especifica un conjunto de operadores en función de su utilización.
Operadores de valores lógicos:
Negación lógica: ¬x, se indica como NOT( x ) ó NO( x ).
Operador Y lógico: se indica como x AND y, o también x Y y. Esta expresión devuelve verdadero cuando x e y son verdaderos.
Operador O lógico: se indica como x OR y, o también x O y. Esta expresión sólo devuelve falso cuando ambas son falsas.
Operadores aritméticos: Se aplican sobre Enteros, y Reales, permitiendo obtener valores numéricos como resultado.
suma aritmética: x + y
resta aritmética: x - y
multiplicación: x * y
división real: x / y
división entera: x / y (cuando x e y son de tipo Entero)
x % y: resto de la división entera
Operadores relacionales: Relacionan valores numéricos para obtener valores lógicos:
![]() : x mayor que y.
: x mayor que y.
![]() : x menor que y.
: x menor que y.
![]() : x mayor o igual que
y.
: x mayor o igual que
y.
![]() : x menor o igual que
y.
: x menor o igual que
y.
![]() : x igual a y.
: x igual a y.
![]() : x distinto de y.
: x distinto de y.
Las funciones son identificadores de operaciones que no se pueden representar con operadores. Para invocar a una función se coloca su nombre, y entre paréntesis los datos sobre los que se aplica. Los siguientes se encuentran en la librería std.math.
|
NOMBRE |
SIGNIFICADO |
|
ABS( x ) |
Valor absoluto Z N o R R |
|
SiN( X ) |
Seno R R (Radianes) |
|
COS( X ) |
Coseno R R (Radianes) |
|
TAN( X ) |
Tangente R R (Radianes) |
|
AsiN( X ) |
Arcoseno R R (Radianes) |
|
ACOS( X ) |
Arcoseno R R (Radianes) |
|
ATAN( X ) |
Arcotangente R R (Radianes) |
|
Log( X ) |
Logaritmo Neperiano R R |
|
LOG10( X ) |
Logaritmo decimal (base 10) R R |
|
Exp( x ) |
E elevado a x: R R |
|
sqrt(X) |
Raiz cuadrada de x: R R |
Además, están disponibles los números especiales PI y E, como constantes para ser usadas en cualquier cálculo.
En ciertas ocasiones puede ocurrir
que no se disponga de una función que realice un determinado
cálculo
necesario. En ese caso deben buscarse las propiedades matemáticas
que permitan realizar la funcionalidad deseada mediante la
combinación de funciones y operadores existentes. Un caso
concreto
es el caso del ![]() que debe ser calculado mediante la propiedad siguiente:
que debe ser calculado mediante la propiedad siguiente:
![]()
En una asignación hay una serie de reglas que rigen el cálculo del efecto de la operación. A continuación se numeran las más importantes:
En la parte izquierda solo puede existir una variable.
La variable pierde su antiguo valor.
La ejecución de una instrucción de asignación comienza con la evaluación de la expresión de la derecha, una vez evaluada se hace efectiva la asignación. Esto implica que si la variable asignada aparece a la derecha se usará su antiguo valor para evaluar la expresión.
ALGORITMO EjecuciónAsignación
CONSTANTES
X: Entero = 2
Y: Entero = 5
VARIABLES
Z: Entero
INICIO
Z y + x
Z z + z
ESCRIBIR( z )
FIN_ALGORITMO
El tipo de dato al que pertenece el resultado de la evaluación de la expresión (parte derecha) debe ser el mismo que el de la derecha de la variable (parte izquierda).
INICIO
z 1
z ( x + y )* Z; /* Equivalente z (x+y)* 1*/
ESCRIBIR( z )
FIN_ALGORITMO
Se utilizan las siguientes instrucciones para publicar información en la pantalla, y obtener información por el teclado, respectivamente.
ESCRIBIR( “Introduzca el radio del círculo” )
LEER( x )
Nótese que, cuando se pide información por el teclado, es conveniente mostrar primero un mensaje que indique qué es lo que hay que introducir (sobre todo si se tiene en cuenta la alternativa, una pantalla vacía con un cursor parpadeante).
ALGORITMO ÁreaCírculo
CONSTANTES
PI: Real = 3.1416
VARIABLES
radio: Real
resultado: Real
INICIO
ESCRIBIR( “Introduzca el radio: ” ); LEER( radio )
resultado ← PI * radio * radio
ESCRIBIR( “El área es: ”, resultado )
FIN_ALGORITMO
El paradigma de programación estructurado nació en los años 60, desde que en 1954 John Backus en IBM comenzó el desarrollo de Fortran, un lenguaje de programación que hoy está prácticamente en desuso. El testigo lo recogieron en su momento lenguajes de programación como Ada, o Pascal, y después lenguajes de programación modernos como C.
Una instrucción es cada uno de los pasos que da un algoritmo para llegar a un resultado. El programador debe tratar de reducir, siempre que sea posible, el número de INSTRUCCIONES y de DATOS empleado, buscando eficiencia.
Instrucción nula es aquella instrucción que no hace nada. Se denota por SEGUIR. Esta instrucción, no se colocará nunca en pseudocódigo pero será empleada en especificación de software para describir formalmente algunas construcciones algorítmicas.
La composición de instrucciones es la forma de agrupar o combinar instrucciones de tal manera que se obtenga el comportamiento deseado. Así es la composición para un autor de música.
Hace referencia a varias instrucciones que se ejecutan una después de otra y en un determinado orden. Esto implica el uso del carácter ‘;’ para la separación de las instrucciones. Ejemplo:
x ← x + 1
x ← x / 2; y ← x % 2
Se trata de composiciones que permiten escoger una secuencia de instrucciones u otra en función de expresiones lógicas o numéricas.
Permite la ejecución o no de una composición de acciones en función de una expresión cuyo valor es de tipo lógico. Su sintaxis es la siguiente:
SI expresión_lógica
composición_de_instrucciones
FINSI
A continuación, se muestra un ejemplo que presenta esta construcción.
ALGORITMO MayorEdad
CONSTANTES
MayoriaEdad: Entero = 18
VARIABLES
edad: Natural
INICIO
ESCRIBIR( “Introduzca una edad: ” ); LEER( edad )
SI edad > MayoriaEdad
ESCRIBIR( “Mayor de edad” )
FINSI
FIN_ALGORITMO
Permite especificar la ejecución de una composición de instrucciones si se cumple la condición u otra distinta si no se cumple la condición. Su sintaxis es la siguiente:
SI expresión_condicional
composición_de_instrucciones1
SINO
composición_de_instrucciones2
FINSI
A continuación, se muestra un ejemplo que presenta esta construcción.
ALGORITMO Máximo
VARIABLES
a: Entero;
b: Entero;
INICIO
ESCRIBIR( “Introduzca un número: ” ); LEER( a )
ESCRIBIR( “Introduzca un número: ” ); LEER( b )
SI a > b
ESCRIBIR( “a es mayor que b” )
SINO
ESCRIBIR( “b es mayor que a” )
FINSI
FIN_ALGORITMO
Instrucción que permite discriminar entre la ejecución de varias composiciones de instrucciones en función del valor de una expresión generalmente numérica. Su sintaxis es la siguiente:
CASO expresión SEA
valor1: COMPOSICIÓN1
valor2: COMPOSiCIÓN2
valor3: INICIO
COMPOSiCIÓN3
FIN
....
valorN: COMPOSICIÓNn
[SINO:composición_defecto]
FIN_CASO
Un ejemplo de utilización de la estructura de decisión alternativa se muestra a continuación.
ALGORITMO Mes
VARIABLES
mes: Entero
INICIO
ESCRIBIR( “Introduzca número de mes: ” ); LEER( mes )
CASO mes SEA
1: ESCRIBIR( “Enero.” )
2: ESCRIBIR( “Febrero.” )
3: ESCRIBIR( “Marzo.” )
4: ESCRIBIR( “Abril.” )
5: ESCRIBIR( “Mayo.” )
6: ESCRIBIR( “Junio.” )
7: ESCRIBIR( “Julio.” )
8: ESCRIBIR( “Agosto.” )
9: ESCRIBIR( “Septiembre.” )
10: ESCRIBIR( “Octubre.” )
11: ESCRIBIR( “Noviembre.” )
12: ESCRIBIR( “Diciembre.” )
SINO: ESCRIBIR( “ERROR: No existe tal mes.” )
FIN_CASO
FIN_ALGORITMO
En caso de que se emplee una composición secuencial para cada caso puede aplicarse el siguiente esquema;
CASO EXPRESIÓN SEA
1: INICIO
INSTRUCCIÓN1
INSTRUCCIÓN2
...
FIN
FIN_CASO
Las estructuras de decisión tienen varias equivalencias, que es interesante tener en cuenta aunque finalmente nunca se usen en un algoritmo.
|
SI C I FIN_SI |
SI C I SINO SEGUIR FIN_SI |
|
SI C I1 SINO I2 FIN_SI |
SI C I1 FIN_SI SI NO( c ) I2 FIN_SI |
|
CASO E SEA A: I1 B: I2 SINO: In FIN_CASO; |
SI E=A I1 SINO SI E=B I2 SINO In FIN_SI FIN_SI |
La última de ellas, sin embargo, sí es posible que se utilice en la vida real. La gran mayoría de lenguajes de programación limitan el uso de la estructura de decisión alternativa o múltiple a que la expresión de control sea de tipo Entero, no permitiéndose el tipo Real ni Cadena, de manera que es necesario realizar la transformación dada.
Provocan una repetición de una instrucción o secuencia varias veces. Hay tres tipos de composiciones iterativas: MIENTRAS, REPETIR, DESDE.
Es una estructura iterativa que permite repetir una instrucción o conjunto de instrucciones mientras se cumpla una condición . La composición iterativa MIENTRAS es la más básica de las composiciones y cualquiera de las composiciones iterativas puede ser reemplazada por ella. Su sintaxis es la siguiente:
MIENTRAS EXPRESIÓN_BOOLEANA
COMPOSICIÓN
FIN_MIENTRAS
El cálculo del factorial se muestra a continuación como ejemplo. El factorial de un número n, o n!, se calcula multiplicando todos los números naturales precedentes a n, hasta 1, incluyendo al propio n. Así, 5! es 5 x 4 x 3 x 2 x 1 = 120.
ALGORITMO Factorial
VARIABLES
numero: Entero
resultado: Entero
i: Entero
INICIO
LEER( numero )
resultado ← numero
i ← numero – 1
MIENTRAS i > 1
resultado ← resultado * i
i ← i - 1
FIN_MIENTRAS
FIN_ALGORITMO
Es muy similar a la anterior, con la salvedad de que la expresión lógica no es una condición de permanencia sino una condición de salida y además el cuerpo se ejecuta como mínimo una vez. Su sintaxis es la siguiente:
REPETIR
composición
HASTA expresión_condicional
Un ejemplo se muestra a continuación:
ALGORITMO SumaNúmeros;
VARIABLES
numero: Entero
resultado: Entero
INICIO
resultado ← 0
REPETIR
LEER( numero )
resultado ← resultado + numero
HASTA numero = 0
ESCRIBIR( “La suma es: “, resultado )
FIN_ALGORITMO
Permite ejecutar una composición para un conjunto de valores conocido. Para ello incorpora una variable llamada vcb (variable controladora del bucle, de tipo entero), de la cual se puede conocer su valor durante la ejecución del bucle y así saber el número de vuelta actual. Su sintaxis es la siguiente:
DESDE vcb ← Vi HASTA Vf [INCREMENTO delta]
composición
FIN_DESDE
Donde:
vcb: variable controladora del bucle
vi: valor inicial
vf: valor final
delta: cuánto aumenta o disminuye vcb por pasada
Ejemplo:
ALGORITMO TablaMultiplicar
VARIABLES
i: Entero
numero: Entero
INICIO
LEER( numero );
DESDE i ← 0 HASTA 10
ESCRIBIR( numero,” x “, i, “=”, numero * vcb )
FIN_DESDE
FIN_ALGORITMO
La composición iterativa MIENTRAS puede representar a cualquier otra composición iterativa. Por ejemplo, una composición DESDE:
DESDE vcb ← Vi HASTA Vf INCREMENTO delta
composición
FIN_DESDE
se puede representar de la siguiente forma:
vcb ← Vi
MIENTRAS vcb <= Vf
composición
vcb ← vcb + delta
FIN_MIENTAS
En el caso de contar hacia atrás, simplemente sería necesario cambiar el signo + y el operador relacional de la condición de permanencia.
En el caso de la composición REPETIR,
REPETIR
I
HASTA expresión_condicional
esta, se podría representar mediante la siguiente combinación de MIENTRAS
I;
MIENTRAS NO( expresión_condicional )
I;
FIN_MIENTRAS;
H asta
aquí hemos visto la notación algorítmica conocida
como
pseudocódigo. Pero además de, esta existen más:
asta
aquí hemos visto la notación algorítmica conocida
como
pseudocódigo. Pero además de, esta existen más:
Pseudocódigo → representación algorítmica estructurada
Diagramas N-S o Nassi Schederman
Diagramas de flujo o flujogramas. → representación algorítmica no estructurada.
Se basa en una representación gráfica de la algorítmica y en el uso embebido de instrucciones pseudocódigo
ALGORITMO: Suma
|
INICIO |
|
LEER( a ) |
|
LEER( b ) |
|
ESCRIBIR( a + b ) |
|
FIN |
CONDICIONAL
|
LEER( a, b ) |
|
|
SI NO |
|
|
ESCRIBIR( a ) |
ESCRIBIR( b ) |
MIENTRAS
|
LEER( x ) |
|
|
resultado ← 0 |
|
|
i ← x - 1 |
|
|
MIENTRAS x > 1 |
|
|
|
resultado ← resultado * i |
|
i ← i - 1 |
|
DESDE
|
LEER( x ) |
|
|
resultado ← 0 |
|
|
DESDE i ← x - 1 HASTA 1 |
|
|
|
resultado ← resultado * i |
REPETIR
|
|
resultado ← resultado * i |
|
i ← i - 1 |
|
|
REPETIR HASTA i = 0 |
|
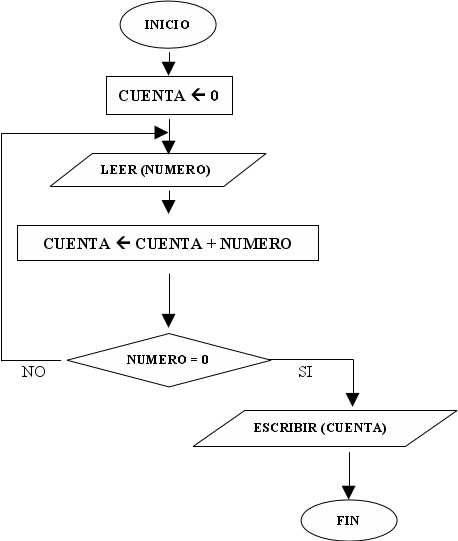
Ejemplo:
|
INICIO |
|
|
resultado ← 0 |
|
|
|
LEER ( num ) |
|
resultado ← resultado + num |
|
|
REPETIR HASTA num = 0 |
|
|
ESCRIBIR ( resultado ) |
|
|
FIN |
|
Simbología:
 Líneas
de flujo que son unidireccionales
Líneas
de flujo que son unidireccionales
INSTRUCCIÓN

Marcan el inicio y el fin del algoritmo:


Ejemplo:
ALGORITMO MCD
{ Este algoritmo permite calcular el MCD de dos números }
VARIABLES
a, b: Entero
INICIO
LEER( a, b )
MIENTRAS a <> b
SI a > b
a ← a – b ;
SINO
b ← b - a ;
FIN_SI
FIN_MIENTRAS
ESCRIBIR( “El mcd es: “, a )
FIN_ALGORITMO
ALGORITMO MCM;
{ Este algoritmo permite calcular el MCM de dos números }
VARIABLES
a: Entero
b: Entero
aCopia: Entero
bCopia: Entero
INICIO
LEER( a, b )
aCopia ← a
bCopia ← b
MIENTRAS a <> b
SI a > b
a ← a – b
SINO
b ← b - a
FIN_SI
FIN_MIENTRAS
ESCRIBIR( “El mcm es: “, ( aCopia * bCopia ) / a )
FIN_ALGORITMO
ALGORITMO Potencia
{ Este algoritmo permite calcular una potencia }
VARIABLES
base: Entero
exp: Entero
resultado: Entero
INICIO
LEER( base, exp )
resultado ← 1
MIENTRAS exp > 0
resultado ← resultado * base
exp ← exp - 1
FIN_MIENTRAS
ESCRIBIR( “El resultado es: “, resultado )
FIN_ALGORITMO
ALGORITMO areas;
{ Este algoritmo permite calcular el área de un cuadrado, de un círculo o de un triángulo }
CONSTANTES
PI: Real = 3,14
VARIABLES
a, b: Real;
{________|_Circulo_|_Cuadrado_|_Triángulo_}
{____a___|__radio__|___lado___|____base___}
{____b___|_________|__________|___altura__}
opcion: Entero
INICIO
REPETIR
ESCRIBIR( “1. Área del cuadrado” )
ESCRIBIR( “2. Área del círculo” )
ESCRIBIR( “3. Área del triángulo” )
ESCRIBIR( “4. Salir” )
ESCRIBIR( “Introduzca la opción: ” )
LEER( opcion )
CASO opcion SEA
1: INICIO
ESCRIBIR( “Introduzca lado: “)
LEER( a )
ESCRIBIR( “Área: “, a * a )
FIN;
2: INICIO
ESCRIBIR( “Introduzca radio: “ )
LEER( a )
ESCRIBIR( “Área: “, a * a * PI )
FIN;
3: INICIO
ESCRIBIR( “Introduzca la base: “ )
LEER( a )
ESCRIBIR( “Introduzca la altura: ”)
LEER( b )
ESCRIBIR( “Área: “, a * b )
FIN;
4: SEGUIR;
SINO: ESCRIBIR( “Opción inválida” )
FIN_CASO
HASTA opcion=4
FIN_ALGORITMO
ALGORITMO leerEnBaseX;
{ Este algoritmo permite obtener el valor decimal
de un número codificado en la base indicada en la constante
Base
}
CONSTANTES
Base: Entero = 2;
VARIABLES
{ variable conteniendo el peso de cada cifra del número }
vcbPeso: Entero;
{ variable auxiliar para calcular el valor acumulado por cifra }
vcbPotencia: Entero;
{ variable auxiliar conteniendo el valor acumulado de cada cifra }
valorPotencia: Entero;
{ número en base Base leído como una cadena }
numStr: Cadena;
{ valor numérico decimal del número }
valorNumero: Entero;
{ Funciones necesarias (variarán de un lenguaje a otro):
length() → devuelve el tamaño de una cadena
val() → devuelve el valor numérico dentro de una cadena
substring() → devuelve una subcadena
}
INICIO
ESCRIBIR( “Dame el número a calcular: “ ); LEER( numStr )
valor ← 0
DESDE vcbPeso ← 1 HASTA length( numStr )
{ Calcular base elevado a vcbPeso - 1 }
valorPotencia ← 1
DESDE vcbPotencia ← 1 HASTA vcbPeso - 1
valorPotencia ← valorPotencia * Base
FIN_DESDE
{Calcular el valor de la cifra }
valorNumero valorNumero +
( valorPotencia
* val( substring( numStr, vcbPeso, 1 ) ) )
FIN_DESDE
ESCRIBIR( “El valor del número es: “, valorNumero )
FIN_ALGORITMO
El pseudocódigo pretende ser un lenguaje de programación de muy alto nivel, que permite desarrollar ideas sin necesidad de llegar al nivel de detalle de un lenguaje real, pero siendo, a la vez, muy sencillo realizar el paso final de traducir a cualquier lenguaje.
Como ejemplo, el algoritmo del máximo divisor común consiste en ir reduciendo al mayor de ambos con el otro, hasta llegar a un punto en el que no se pueda reducir más. Supóngase el siguiente algoritmo:
ALGORITMO mcd;
VARIABLES
a, b: Entero;
INICIO
LEER( a, b );
MIENTRAS a <> b
SI a>b
a ← a – b
SINO
b ← b – a
FIN_SI
FIN_MIENTRAS
ESCRIBIR( ‘MCD=’, a )
FIN_ALGORITMO
Podría ser codificado fácilmente en distintos lenguajes de programación. Por ejemplo, a continuación se muestra el algoritmo codificado en BASH (un lenguaje de scripting para UNIX):
#!/bin/bash
# mcd
echo –n ‘Introduce a: ’
read a
echo –n ‘Introduce b: ’
read b
while test ! $a -eq $b
do
if test $a -gt $b
then
a=`expr $a - $b`
else
b=`expr $b - $a`
fi
done
echo “El MCD es $a”
El mismo algoritmo escrito en C++ sería:
// mcd
#include <cstdio>
int main()
{
printf( "Introduce a: " );
scanf( "%d",&a );
printf( "Introduce b: " );
scanf( "%d",&b );
while ( a != b ) {
if ( a > b )
a = a - b;
else b = b - a;
}
printf( "El MCD es %d", a );
}
Por otra parte, en Pascal sería:
program mcd;
var
a, b: integer;
begin
write( 'Introduce a: ' );
readln( a );
write( 'Introduce b: ' );
readln( b );
while a <> b do
if a > b then
a := a - b
else b := b - a;
writeln( ‘El MCD es ’,a );
end.
En cuanto a lenguajes dinámicos, en Ruby sería:
# mcd
print "Introduce a: "
a = gets.to_i
print "Introduce b: "
b = gets.to_i
while a != b
if a > b
a = a - b
else b = b – a end
end
print "El MCD es ", a, "\n"
Mientras que en Python, se escribiría:
# mcd
a = input( "Introduce a: " )
b = input( "Introduce b: " )
while ( a != b ):
if ( a > b ):
a = a - b
else: b = b - a
print "MCD = ", a
Lo que se pretende demostrar con esto es que los lenguajes estructurados emplean distintas notaciones para representar composiciones secuenciales, iterativas o de decisión. Sin embargo, todos los lenguajes tienen los mismos elementos, que están también presentes en la notación algorítmica..
En este sentido, dada la diferencia de los lenguajes y su carácter estricto, resulta muy interesante emplear una notación algorítmica que va a resultar más flexible para poder construir los algoritmos y, una vez construido el algoritmo, fijarse en los detalles del lenguaje de programación.
A continuación, se muestra el mismo programa en jC:
import std.io;
import std.util;
import std.string;
int a = strToInt( readln( "Introduce a: " ) );
int b = strToInt( readln( "Introduce b: " ) );
while ( a != b ) {
if ( a > b ) {
a = a - b;
}
else {
b = b - a;
}
}
write( "El MCD es: ");
writeln( a );
Dado que el pseudocódigo no es más que un lenguaje genérico, y que todo lo que se puede hacer en pseudocódigo se puede hacer en cualquier lenguaje de programación, la traducción de uno a otro debería ser más o menos automática. En esta sección, se comentarán las construcciones más comunes en pseudocódigo, y se mostrará su equivalente en lenguaje jC.
Estos son los elementos más básicos disponibles en programación. Muchos de estos elementos básicos, pueden no tener traducción en algunos lenguajes de programación, mientras otros requieren de más líneas de código.
|
Pseudocódigo |
jC |
|
{ comentario } |
/* comentario */ |
|
ALGORITMO ejemplo |
/** @name Ejemplo */ |
|
Verdadero, V o T |
true |
|
Falso, o F |
false |
|
a ← 5 |
a = 5; |
|
( a = 5 ) |
( a == 5 ) |
A continuación se muestran algunos valores literales que pueden aparecer en un cualquier programa.
|
Pseudocódigo |
jC |
Ejemplo de uso |
|
“Esto es una cadena” |
“Esto es una cadena” |
writeln( “Hola, mundo” ); |
|
5 |
5 |
x = 5; |
|
3.14 |
3.14 |
area = radio * radio * 3.14; |
|
'd' |
'd' |
char letraDe = 'd'; |
Es necesario que un programa se comunique con el usuario. Para ello, normalmente se tienen determinadas funciones disponibles en la biblioteca estándar del lenguaje.
|
Pseudocódigo |
jC |
Ejemplo de uso |
|
ESCRIBIR( “¡Hola!” ) |
write(), writeln() print(), println() |
printf( “¡Hola!” ); |
|
LEER( x ) |
readln() |
x = intToStr( readln() ) |
En programación, las constantes y variables están normalmente ligadas a un tipo de datos (aunque en posteriores cursos se estudiarán lenguajes no tipados). A continuación, se muestran los tipos de datos fundamentales. La mayor parte de las veces, los lenguajes de programación permiten escoger entre tipos de datos más específicos, aunque todos permiten representar, al menos los fundamentales, que son los que se usan en pseudocódigo, y que se enumeran a continuación.
|
Pseudocódigo |
jC |
Ejemplo en jC |
|
Entero |
int |
int x; x = 5; int numRuedas = 4; |
|
Real |
double |
float radio = 4.56; double distancia = 10.8967; |
|
Lógico |
bool |
bool hecho = true; |
|
Carácter |
char |
char x = 'r'; |
|
Vector, Matriz |
Tipo[maxElementos] |
int x[20]; |
|
Cadena |
char nombre[] |
char saludo[64]; strcpy( saludo, “¡Hola, mundo!” ); |
|
Constantes |
final tipo nombre... |
final double PI = 3.1415927; |
Una nota aparte merecen, en el lenguaje jC, las cadenas, que en realidad no son sino vectores de caracteres. Es necesario crear un vector de caracteres para cualquier cadena, con una longitud suficiente para albergarla. Como con todos los vectores, para poder calcular el tamaño de una cadena se utiliza la función size(). Finalmente, los vectores tienen siempre su primer elemento en 0, y lógicamente su última posición es la longitud del vector menos uno. Así, un vector de 3 elementos presenta las posiciones 0, 1, y 2.
/**
@name EjemploCadenas
@brief Muestra varias formas de manejar cadenas (char[])
@author jbgarcia@uvigo.es
*/
import std.io;
import std.util;
char[] cadHola = new char[4];
char[] cadAdios = "Adiós";
cadHola[ 0 ] = 'H';
cadHola[ 1 ] = 'o';
cadHola[ 2 ] = 'l';
cadHola[ 3 ] = 'a';
print( "Longitud: " );
print( size( cadHola ) );
print( ": " );
println( cadHola );
print( "Longitud: " );
print( size( cadAdios ) );
print( ": " );
println( cadAdios );
En el ejemplo anterior se muestran dos formas de crear cadenas, mostrando que efectivamente, no son otra cosa que vectores de caracteres.
Se ha mostrado que el pseudocódigo tiene una serie de partes fundamentales, que en el caso del lenguaje de programación jC son bastante más flexibles. Simplemente, la primera instrucción tras los import es la primera del programa. Si existe alguna constante, eso sí, debe ser creada entre los import y dicha primera instrucción.
ALGORITMO ÁreaDelCirculo
{ Calcula el área del círculo, pidiendo el radio por teclado }
CONSTANTES
PI: Real = 3.1415927
VARIABLES
radio : Real
INICIO
ESCRIBIR( “Introduzca el radio:” )
LEER( radio )
ESCRIBIR( “El resultado es: “, radio * radio * PI )
FIN_ALGORITMO
La implantación en jC es la siguiente:
/** @name AreaCirculo
@brief Calcula el área del círculo
@author jbgarcia@uvigo.es
*/
import std.util;
import std.io;
import std.math;
import std.string;
double radio = strToDbl( readln( "Introduce radio: " ) );
double resultado = PI * radio * radio;
print( "Superficie: " );
println( resultado );
La composición secuencia consiste, simplemete, en poner una instrucción a continuación de la otra, como se observa a continuación:
|
Pseudocódigo |
C++ |
|
i ← 1; ESCRIBIR( i ) |
i = 1; printf( “%d”, i ); |
La composición condicional, segunda característica clave de la programación estructurada, consiste en permitir realizar decisiones según se cumpla una condición o no.
|
Pseudocódigo |
C++ |
|
SI x>10 x ← x - 1 j ← j + 1 FIN_SI
|
if ( x > 10 ) { x = x + 1; j = j + 1; } |
|
SI x>y x ← x – y SINO y ← y - x FIN_SI |
if ( x > y ) { x = x – y; } else { y = y – x; } |
Un caso particular de la composición condicional es la selección entre varios valores simples (enteros, lógicos o enumerados), una posibilidad presente en muchos lenguajes de programación.
|
Pseudocódigo |
C++ |
|
CASO x SEA 1, 2:INICIO x ← x + 1; y ← y - 1; FIN 3: y ← y + 1; SINO: z ← z – 2; FIN_CASO
|
switch( x ) { case 1: case 2: x = x + 1; y = y – 1; break; case 3: y = y + 1; break; default: z = z – 2; }
|
Finalmente, el tercer gran pilar de la programación estructurada es la repetición. A continuación se muestran las construcciones más frecuentes y su traducción, en C++.
|
Pseudocódigo |
C++ |
|
MIENTRAS x > 5 x ← x / 2; y ← y – 1; FIN_MIENTRAS |
while ( x > 5) { x = x / 2; y = y – 1; } |
|
REPETIR LEER( x ); HASTA x < 5; |
do { scanf( “%d”, &x ); } while( x >= 5 ); |
|
DESDE i ← 1 HASTA 10 ESCRIBIR( i ) FIN_DESDE |
for(i = 1; i <= 10; ++i) { printf( “%d”, i ); } |
A continuación, se muestran varios ejercicios de los planteados a lo largo de este capítulo, resueltos.
El cálculo del factorial. El factorial de un número n, o n!, se calcula multiplicando todos los números naturales precedentes a n, hasta 1, incluyendo al propio n. Así, 5! es 5 x 4 x 3 x 2 x 1 = 120.
/**
@name Factorial
@brief Computa el factorial de un num.
@author jbgarcia@uvigo.es
*/
import std.io;
import std.string;
int num = strToInt( readln( "Dame un numero: " ) );
int resultado = num;
--num;
while( num > 0 ) {
resultado *= num;
--num;
}
print( "El resultado es: " );
println( resultado );
El cálculo de varias áreas. Realizar un programa que permita calcula la superficie de varias figuras, como el cuadrado, el círculo y el triángulo rectángulo.
/**
@name Areas
@brief Computa la superficie de varias figuras.
@author jbgarcia@uvigo.es
*/
import std.io;
import std.string;
import std.util;
import std.math;
double a = 0;
double b = 0;
int opcion = 0;
do {
println( "1. Superficie del cuadrado." );
println( "2. Superficie de la circunferencia." );
println( "3. Superficie del triangulo rect." );
println( "0. Salir." );
opcion = strToInt(
readln( "Introduza superficie a calcular: " ) );
switch( opcion ) {
case 0:
println( "Terminando..." );
break;
case 1:
a = strToInt( readln( "Introduzca lado: " ) );
print( "Superficie: " );
println( a * a );
break;
case 2:
a = strToInt( readln( "Introduzca radio: " ) );
print( "Superficie: " );
println( a * a * PI );
break;
case 3:
a = strToInt( readln( "Introduzca base: " ) );
b = strToInt( readln( "Introduzca altura: " ) );
print( "Superficie: " );
println( ( a * b ) / 2 );
break;
default:
println( "Entrada incorrecta." );
break;
}
} while( opcion != 0 );
println( "Fin" );
Los ejercicios presentados aquí deben realizarse siempre primero escribiendo el pseudocódigo, y después programando el algoritmo en jC. En la mayoría de los casos, sin embargo, puede encontrarse el algoritmo ya diseñado en las páginas de este mismo capítulo.
Amplia el ejercicio del cálculo de las áreas para que permita también calcular el área de un rectángulo.
Escribe un programa que, una vez pedido un número x por teclado, visualice la tabla de multiplicar de dicho número.
Calcula el Máximo Común Múltiplo de dos números introducidos por teclado.
Calcula xy, es decir, la potencia de x elevado a y, siendo ambos números introducidos por teclado.
Implanta el algoritmo del cálculo del valor decimal de un número en cualquier base.
Transforma el algoritmo anterior, de tal forma que la base, en lugar de ser un valor constante, se pida también por teclado.